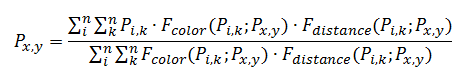Bilateral image filter: .NET implementation

UPDATE 24.02.2012: Starting from version 2.2.4 AForge.NET contains Bilateral filter:http://www.aforgenet.com/news/2012.02.23.releasing_framework_2.2.4.html.

In the previous post you may find an overview of bilateral image filtering and sample results it can produce. In this post you'll find out about my implementation and links to the files.

The first thing to mention is that my implementation relies on AForge.NET (version 2.2.3) framework which is a massive framework for image and video processing, solving AI and recognition tasks etc. One of the framework parts is dedicated to image processing and the filter fitted it pretty well.

If you don't use AForge.NET and don't want to download the full library then you may use an archive from here. Since only a small part of AForge.NET is used you'll need to reference 3 assemlblies:

• AForge.dll
• AForge.Math.dll
• AForge.Imaging.dll

The acrhive contains the following folders:

• FilterDemoExecutable - compiled demo of a filter. It's based on AForge.NET filter demo so it also has a large number of other AForge filters. The differences are: Bilateral filter, saving files, copy the processed image to clipboard.
• FilterDemo - source for the above application.
• Release - all assemblies required (as listed above)
  
• Sources - solution with AForge.Imaging.dll sources which includes Bilateral filter (class AForge.Imaging.Filters.Smooting.Bilateral). Other AForge.NET projects are not included so ignore the warning you'll get upon opening the solution.
  

If you are already using AForge.NET then simply add the following .cs file to your project and that would be enough.

If you'd like to play with a demo application only then go here.

Bilateral image filter: Edge preserving blur and noise reduction

Bilateral filter seems to be a very underestimated image improving technique. It's not frequently met across internet. The filter may help with solving the following tasks:

• Noise reduction - pretty utilitarian & usual goal. When you have photos pictured with high ISO or within poor lighting conditions noise reduction will give them a more natural look
• Sharpen edges
  
• Great artistic effects - my favorite part, images processed with bilateral filter get an appealing glossy look
  

In this post I'll try to briefly describe the concept of the filter (in simple words without much math) and present a number of samples showing results that can be achieved.

The next post presents a .NET implementation of the filter.

The genuine article on the filter can be found here.

How it works

Let's start with a sample. Bellow you may see three images (taken from the original article):

• The first (from left to right) is the original photo of a red jacket against blue sky, lots of noise.
• The second image was received after Gaussian blur (that filter can be found in Photoshop and I assume in almost any other photo editor), the edge is blurred while no noise at all.
• The last image is processed by bilateral filter, the edge is sharper, noise is removed.

The above sample is a good demo of the Bilateral filter concept: it blurs only similar areas (domains) while bypassing contrast transitions (edges).

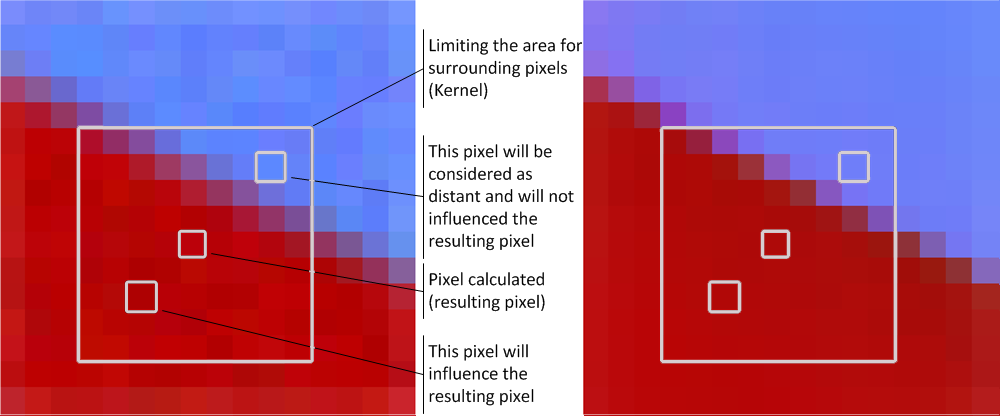
To be more precise Bilateral filter does a pixel-by-pixel evaluation and calculates the color for a specific pixel depending on the colors of surrounding pixels. The influence on the result is determined by the similarity of the surrounding pixels to the processed pixels. There're 2 criteria which define the similarity and "weigh coefficient" for a specific pixel (how much it puts into the result):

• Spatial closeness, i.e. distance between 2 pixels, the further specific pixel stands from the resulting the less it influences it
  
• Color closeness - color difference, black and white are "color distant", so as red and blue (in RGB model) . Due to considering this criterion we get edge preserving, red pixels do not influence blue ones and the edge between areas stays sharp

Assume we do the pixel-by-pixel processing in Gray scale image (one pixel = one byte). For each pixel being calculated we operate with numeric values in range [0;255]. The value for the resulting pixel is calculated as a weighted mean of surrounding pixels were weight is determined by pixel color and spatial functions.

The formula for calculating pixel value is as follows: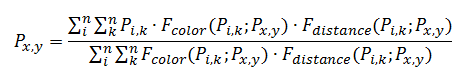

where Px,y - pixel value being calculated, Pi,k - one of the pixels in the surrounding area (kernel), n - surrounding area size (kernel size), Fcolor - function that determines color closeness, Fdistance - determines spatial closeness.

Fcolor, Fdistance are the functions which define the results produced by the filter. They are exponent functions and details on the internals can be found in the article describing bilateral filter. Since it's an iterative algorithm a limited number of pixels takes part in calculation which is determined by the surrounding square (kernel).

The important thing is that there're 3 parameters which influence the functions & algorithm and thus the results. The parameters are positive integral numbers:

• Color Factor - the greater the number is, the greater are the domains and less contrast edges will get blurred.
  
• Spatial Factor - the greater the value is the more blurry effect you'll get in domains, i.e. in areas of the same color.
• Kernel Size (n) - this is an odd number > 1 (3, 5, 7, ...). It limits the set of pixels which take part in computation. This parameter influences performance (large values > 21 can slow the process dramatically) and the general "power" of the filter (low values < 5 on high resolution images may not produce any noticeable results).

Bellow you may see another example of bilateral filter being applied to RGB image. The approach is exactly the same as described above but in this case each channel values for a specific value is calculated separately (instead of one value for gray scale image 3 values are calculated for a pixel):

Filter parameters influencing the output

Bellow you'll find an original image and a grid depicting how the image is changed by the filter depending on specific parameter values, kernel size is 7 and is constant:

Image samples

Original

Kernel = 13, Color = 20, Spatial = 50

Original

Kernel = 15, Color = 7, Spatial = 70 (noise reduction)

Kernel = 19, Color = 20, Spatial = 100 (adding blurry effect)

Original

Kernel = 21, Color = 7, Spatial = 100 (noise reduction)

Kernel = 21, Color = 21, Spatial = 100 (adding blurry effect)

Original

Kernel = 25, Color = 10, Spatial = 70 (noise reduction)

Kernel = 25, Color = 20, Spatial = 70 (adding blurry effect)

Original

Kernel = 25, Color = 20, Spatial = 70 (adding blurry effect)

Avoid Wikipedia Janurary 18th 2012 blackout

As you could possibly notice Wikipedia's home page (en.wikipedia.org) was not fully disabled and there's full English content blinking prior to the black banner covers it. As it turned out there's a JavaScript added to the page which blocks the landing page:
http://meta.wikimedia.org/w/index.php?title=Special:BannerLoader&banner=blackout&campaign=English+Wikipedia+Blackout&userlang=en&db=enwiki&sitename=Wikipedia&country=BY
- the ending can be a bit different depending on your country, language settings.

To turn off the banner you may use Ad blocker and add a special rule. I use AdBlock Plus with FF, the exception looks the following way:



URL to block: *meta.wikimedia.org/w/index.php?title=Special:BannerLoader&banner=blackout&campaign=English+Wikipedia+Blackout*

Save confirmation when leaving a web page

User story

A user opens a web form, fills in values in input elements, do not click "Save" button and clicks any navigation link. A confirmation message is shown: "There're unsaved changes. Do you wish to save them before navigating away?". If the user clicks "OK" - changes are saved and the desired page is opened. Clicking "Cancel" opens the destination page without saving user input.

Implementation

The idea is to have a JavaScript global object which is capable of tracking changes, can be called by custom JavaScript code (in order to notify the object about changes), which shows confirmation message in case of clicking navigation links and calls back to custom code in order let it do server requests and save data.

The first part is the prototype itself and global object instantiation (mind JQuery is required):

function ChangesTracker () {
    this.confirmMessage =
        "There're unsaved changes on the page. Do you wish to save them before navigating away?";
    this.selectors = ["html body table tbody tr td.Toolbar a"];
    this.ignoreSelectors = ["a#save", "a#remove"];
    this.changedFlag = false;
    this.enabled = false;
    this.eventPublisher = {};
}

ChangesTracker.prototype.setChanged = function (state) {
    this.changedFlag = state;
}

ChangesTracker.prototype.raiseOnLeave = function () {
    if (this.enabled && this.changedFlag == true && this.showConfirmation()) {
        $(this.eventPublisher).trigger("onLeaveWithChanges");
        return true;
    }
    return false;
}

ChangesTracker.prototype.bindOnLeaveEvent = function (handler) {
    $(this.eventPublisher).bind("onLeaveWithChanges", handler);
}

ChangesTracker.prototype.showConfirmation = function () {
    return confirm(this.confirmMessage);
}

ChangesTracker.prototype.enable = function (selectors) {
    var self = this;
    if (selectors) this.selectors = selectors;
    var query = $();

    for (var i in this.selectors) {
        query = query.add(this.selectors[i]);
    }
     
    for (var i in this.ignoreSelectors) {
        query = query.not(this.ignoreSelectors[i]);
    }
 
    query.click(function () {
         self.raiseOnLeave();
     });

    this.enabled = true;
}

ChangesTracker.prototype.disable = function () {
    this.enabled = false;
}

var changesTracker = new ChangesTracker();

$(document).ready(function () {
    changesTracker.enable();
});

The above code can be put to a separate script file and referenced on the pages which require changes tracking. Referencing the script will initialize a global variable changesTracker which is a ready to use obejct. The highlights about the object are:

<script type="text/javascript" src="JavaScripts/ChangesTracker.js"></script>
<script type="text/javascript" language="javascript">
    changesTracker.bindOnLeaveEvent(function () {
        $('form#fields').submit();
    });

    $(document).ready(function () {
        $("#table.fields input").change(function () { changesTracker.setChanged(true) });
    });
</script>

In our case we assume that there's a table with a number of <input> elements in it. The table is placed within a form with id fields. The 2 things we need to do are:

• Notify the tracker about changes
  
• Respond to tracker event and do the save
  

Known issues

1. Not working in IE6 and IE9 in comparability view mode
2. Form validation require minor amendments to the solution above (e.g. bindOnLeaveEvent may need args in order let the tracker know whether to leave the page)